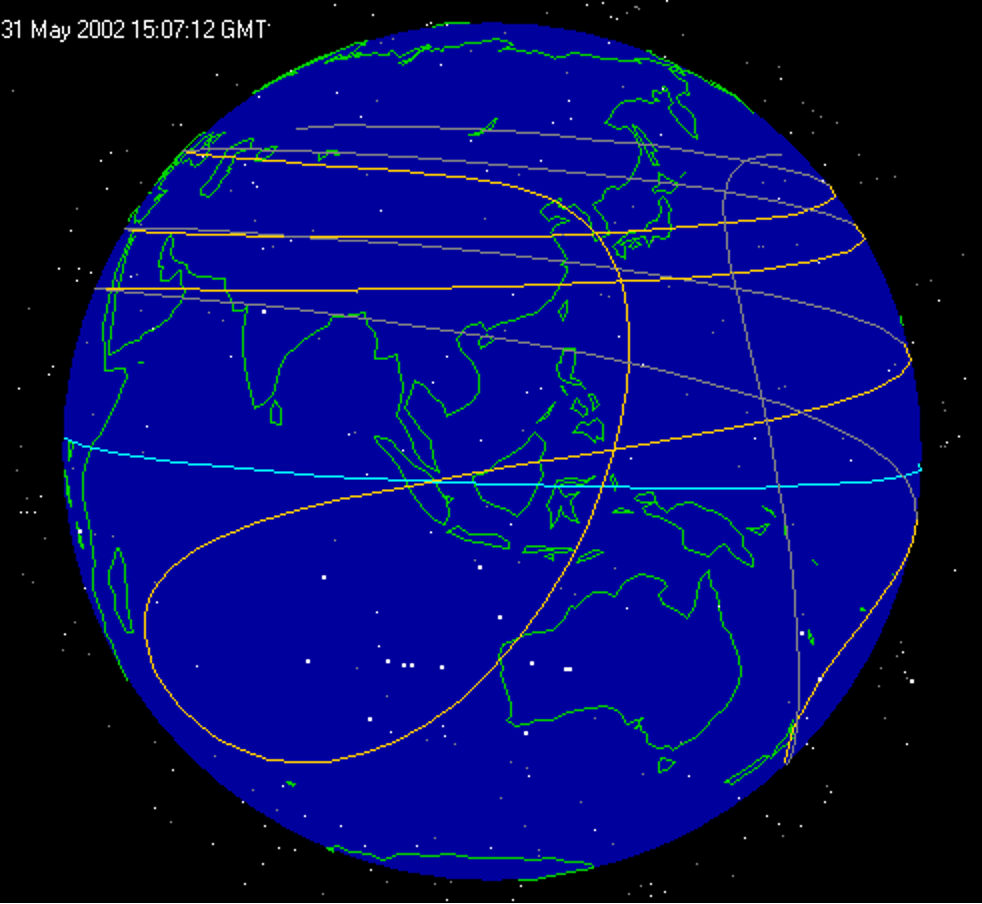
Gary, you still don’t seem to understand what I’ve been saying. I do not disagree with you that the lines “represent” Chandra’s actual flightpath. I’ve said over and over again that a person could use those lines to know where Chandra is located relative to the earth.

Well, Bob, if you agree with me that those lines show us “where Chandra is located relative to the earth,” then you have to explain how an unpowered satellite can move like that “relative to the earth” if the earth is stationary.

But here’s what you are either ignoring, denying or just simply refuse to accept: It is Chandra’s actual flightpath relative to a rotating ground, not a stationary ground.

No, Bob, it is Chandra’s actual flightpath relative to the ground. Period. This is the point you are either “ignoring, denying or just simply refuse to accept,” even though you agreed with me on it one sentence ago. That looping yellow line shows where Chandra really will pass overhead. In other words, whether the earth is rotating or not, that’s where Chandra really will be relative to the ground, and you and I need to be able to account for that actual movement relative to the ground. I can do so quite easily by assuming an elliptical orbit around a rotating earth. But if you assume that the earth isn’t rotating, then I don’t see how you can make a satellite move like that.

If the earth were stationary the lines would be different.

Right, and if the earth rotated sideways or backward they’d be different, too. We could generate dozens of hypothetical flightpaths, but there’s only one flightpath that corresponds to the satellite’s actual flightpath relative to the ground, and that’s what I showed above. That flightpath shows the satellite passing over western Australia, and that means that an astronomer in western Australia would be able to aim his telescope straight up at the appropriate time and see the satellite (assuming, of course, that it passed overhead at night).

That is a fact. Thus, the lines do not prove the earth is rotating. They only prove what the flight path looks like assuming that the earth is rotating. Unless you deal with that point, this dialogue can go no further.

Bob, you just said that these lines represent “where Chandra is located relative to the earth.” In other words, this is its real flightpath over the real ground. If these lines predict that Chandra will pass over Hawaii, then by golly, it will. Therefore, this is not “what the flight path looks like assuming that the earth is rotating,” this is what the flight path looks like. Period. Unless you deal with that point, the dialogue can go no farther.

Previous:

You still don’t seem to get what’s happening here, Bob. That meandering line is Chandra’s actual flightpath over the ground. That’s where you have to aim your telescope if you want to see the satellite. If that line predicts that Chandra will pass over eastern Nevada, on a north-south heading, that means that an astronomer in eastern Nevada would be able to point his telescope straight up at the appointed time and see the satellite. If that line didn’t represent Chandra’s actual flightpath over the ground, astronomers wouldn’t be able to use that ground-track data to aim their telescopes.

Again, this just proves you do not comprehend what I’ve been saying. The only reason he can point his telescope up at the appointed time is because, according the computer-generated chart of Chandra’s flight path (which is based on a rotating earth), the computer will tell him to look at a certain place in the sky over Nevada at a certain time.

Right, because if Chandra is orbiting in an ellipse and if the earth is rotating, then Chandra really will be over a certain place in Nevada at a certain time. But your stationary-earth assumptions would produce a different flightpath than the one the satellite actually follows relative to the ground. Therefore, your stationary-earth assumptions must be wrong.

But if you told the computer that the earth was not rotating and asked it to compute when Chandra was going to be over at Nevada, the computer would give you the exact same time as it would in the rotating earth calculation. That is a fact.

No, it’s not. You just said that “if the earth were stationary the lines would be different.” Well, those lines represent where the satellite is going to be, relative to the ground, at any given time. Different lines mean the satellite is going to be passing over different places at the same time, and that’s not possible. If your line shows the satellite passing over Guam while mine shows it passing over Nevada, they can’t both be right. Therefore, if my lines show where Chandra is really going to be – which you’ve admitted – then my lines reflect the actual motion of the satellite relative to the ground, and you need to explain how an unpowered satellite can move like that if the earth is stationary.

Previous:

Now, it being the case that this is Chandra’s actual flightpath, our two respective systems must explain how a satellite can pass over the surface of the earth in that squiggly, loopy pattern. In my system, the trajectory is easily explained as the superimposition of an elliptical orbit over a rotating earth. But in your system, where the earth doesn’t move, only the satellite moves. Therefore, the satellite must somehow steer itself along that wild, squiggly, loopy course. How does it do that?

 

If you then tell the computer that the earth is stationary and ask it to tell you Chandra’s whereabouts with respect to a specific spot on earth, it will do so, but it will make a chart on the graph which is different than the squiggly lines in Gary’s original graph.

 

Right, and if you then aim your telescope where this new graph predicts the satellite will be, it won’t be there.

You’ve just admitted to the audience that your objection is a mere assertion, since you provided no evidence to back it up. You’ve never asked NASA to provide you with a graph of Chandra’s flight path based on a non-rotating earth, have you? So you have no way of knowing what this graph would show.

Well, it had better show the same spirally, loopy flightpath I showed you above, because that’s the path the satellite actually follows relative to the ground. That’s the trajectory astronomers (who are located on the ground) use to predict when the satellite will be passing overhead. But I can tell you exactly what a satellite’s flightpath would look like based on a non-rotating earth. Every satellite, whether its orbit is highly elliptical or nearly circular, orbits the earth in a specific plane, and we all know that when a plane intersects a sphere it forms a circle around the sphere. Just imagine immersing a white billiard ball halfway into a vat of black ink. The surface of the ink would make a perfect circle around the billiard ball. This is what the intersection of a satellite’s orbital plane with a stationary earth would look like:

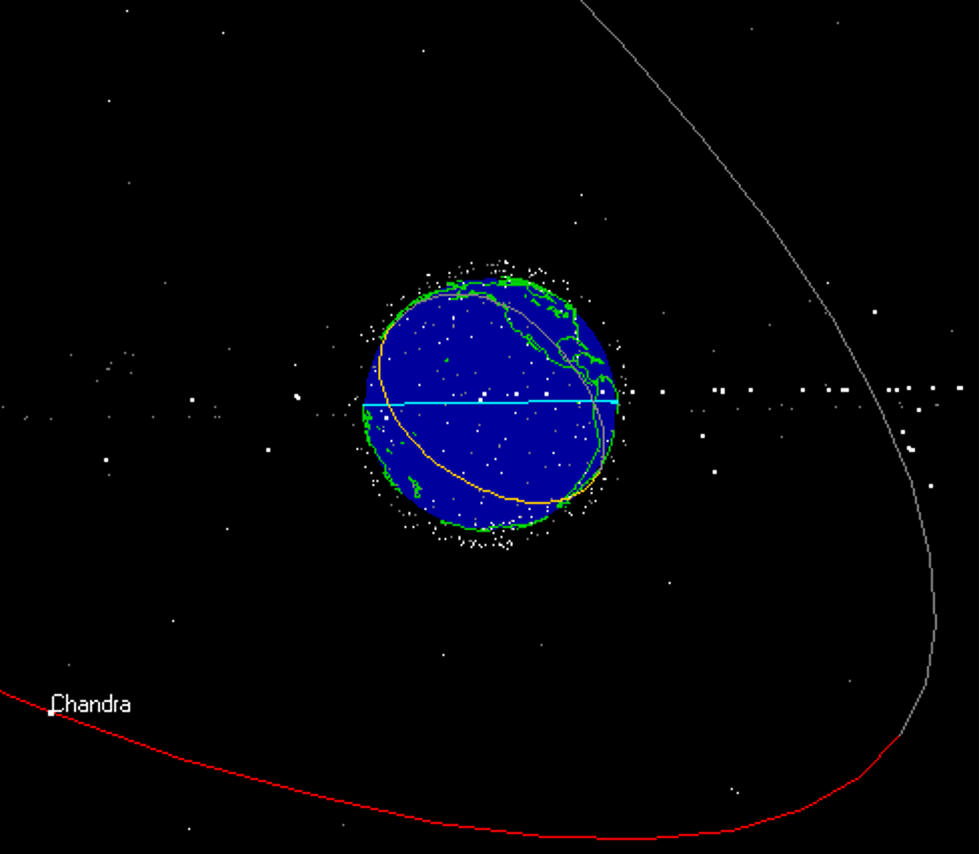
But it’s actual flightpath looks like this:

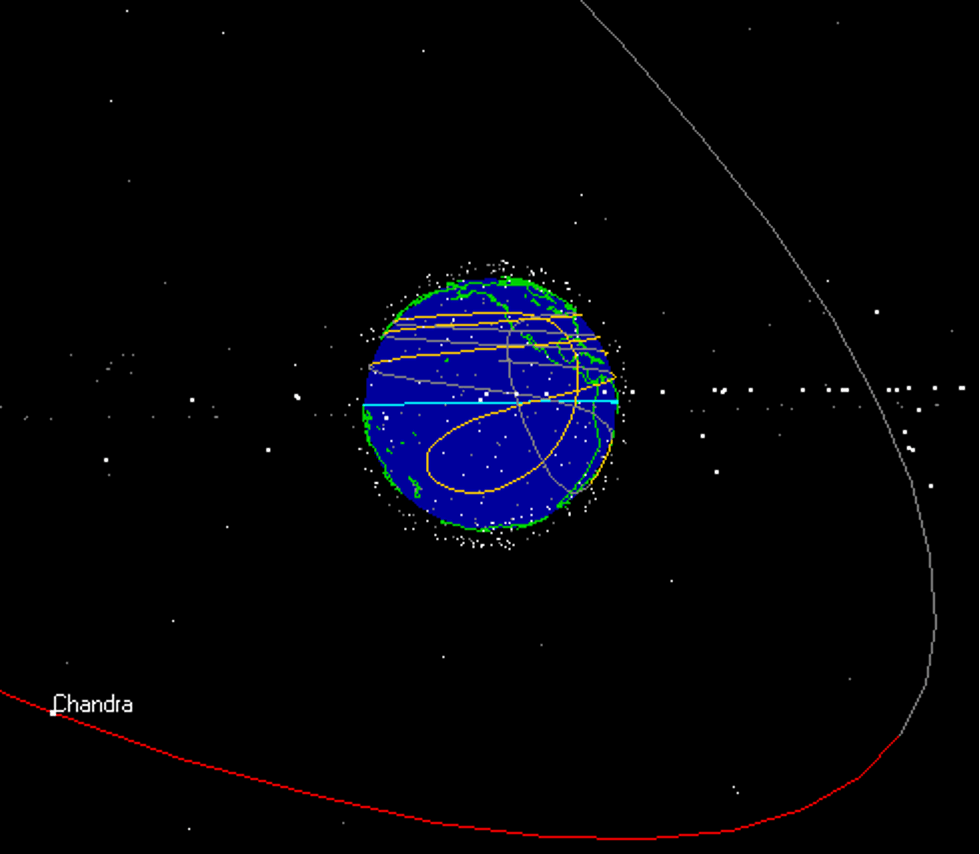
These can’t both be right, Bob. And the fact is, astronomers use the loopy, spirally trajectory to predict when the satellite will pass overhead, which proves that this trajectory represents the real, actual flightpath of the real, actual satellite over the real, actual ground. If you can’t account for that flightpath with stationary-earth assumptions, then the earth must not be stationary.

Previous:

These aren’t graphs of cosmological systems, they’re graphs of the actual flightpath of a satellite relative to the ground. That satellite either passes over the specific places NASA’s graph says it will, or it doesn’t. Under no circumstances, though, can two different ground-tracks both be “true.” One represents where the satellite will pass over the ground; the other does not.

Two ground-tracks can both be right, since one is from a rotating earth and the other from a non-rotating earth.

On the contrary, it’s impossible for two different ground-tracks to both be right. Remember, a ground-track represents where a satellite will actually pass overhead. In other words, if you’re standing somewhere along that predicted ground-track and you look up at the right time, a multi-million dollar spacecraft will be directly above your head. But that satellite can’t be in two different places at the same time. Therefore, two different ground tracks can’t both be right. If your ground-track shows the satellite passing over Japan at the same time my ground-track shows it passing over Nevada, one of those ground-tracks is wrong.

You can prove this for yourself. Hang a can of paint from the ceiling, with a pinhole in the bottom, and swing the paint can in a precise elliptical orbit. Beneath the can of paint, place a basketball. On your first try, let the paint stream from the can onto the basketball without turning the basketball. You’re going to see a simple elliptical paint line made on the basketball. On your second try, put the paint can in the same precise elliptical orbit and let the paint stream from the can onto the basketball while your turning the basketball. You’re not going to see a simple elliptical paint line. You’re going to see that line go all over the basketball, back and forth, and side to side. But neither the paint can nor the basketball has moved its position relative to one another. The only thing that has changed is that the basketball was rotated in one scenario but not the other.

Exactly. And therefore, as you pointed out, the pattern of drops on the basketball is going to be different in each scenario. If a miniature person were standing on the surface of the basketball, he might get hit by a paint drop in the first scenario that would have completely missed him in the second scenario. In fact, if he knew that the paint can was swinging in “a precise elliptical orbit,” he would be able to determine whether the basketball was rotating by observing the pattern of the paint drops. If he saw them fall in “a simple elliptical paint line” on the basketball, he would know that the basketball was stationary. But if he saw them “go all over the basketball, back and forth, and side to side,” he would be able to deduce that the basketball must be rotating. Likewise, because we know that Chandra is orbiting the earth in “a precise elliptical orbit,” and because we can see that it passes over the ground in a spirally, loopy pattern, we can deduce that the ground must be rotating.

Previous:

The point of my previous post, to put it crudely, is that Chandra does not have a big pencil that reaches to the earth and by which it marks out a trajectory.

 

But if it did, it would mark out exactly the trajectory shown on NASA’s maps. Again, the fact that astronomers use this same trajectory data to aim their telescopes proves that Chandra is right where NASA says it will be relative to the surface of the earth.

As the above example shows, it would only mark out that specific trajectory on a rotating earth, not a stationary earth.

That’s right, but the point you’re consistently failing to grasp is that the satellite really does mark out this specific trajectory relative to the surface of the earth! That’s how astronomers are able to find it with their telescopes. They know right where to point them because they know right where the satellite is going to be relative to the ground. The fact that the satellite “would only mark out that specific trajectory on a rotating earth” proves that the earth is rotating, just as surely as the spirally paint patterns in your example prove that the basketball is rotating.

Previous:

No, it only proves that the system they are using will account for Chandra’s whereabouts with respect to a rotating earth, but it does not prove that the system is a reality, that is, that the earth is rotating.

 

Then please tell me how a satellite can follow that squiggly, loopy trajectory over the ground if the earth isn’t rotating. You keep avoiding that question.

No, I don’t avoid the question. I’ve answered it many times. Here’s the rub. It doesn’t follow a squiggly loopy trajectory in a stationary earth. Until you ask NASA to show you a graph of Chandra’s trajectory in a stationary earth, then you really have no basis for making the above statement.

Bob, every time an astronomer successfully uses that “squiggly loopy trajectory” to aim his telescope at Chandra, it proves that that trajectory is correct.

Previous:

Once again, the image we see in NASA’s pictorial is exactly what one would expect to see from a rotating earth. But that doesn’t prove that the earth is rotating. All it proves is that if one assumes a rotating earth, the trajectory will follow the path depicted in the pictorial.

 

No, the satellite follows that trajectory whether the earth rotates or not.

No, Gary hasn’t shown that. He hasn’t asked NASA to produce a pictorial of Chandra’s lines assuming a non-rotating earth. NASA could do so if they wished, or if Gary asked them.

I don’t understand why you’re not getting this, Bob. I showed you a picture of Chandra in orbit taken by Gary Emerson at E.E. Barnard Observatory in Golden, Colorado, using a 25 cm telescope: