It is a fact that in such circumstance earth-orbiting satellites continue to follow the same path when they’re on the side of the earth away from the sun and moon (point A) as they do when they’re between the earth and the sun and moon (point B). That proves that the effects of the sun and the moon on the satellite’s orbit are negligible. Now, you might more plausibly claim that the stars exert a significant influence, because they surround the earth-moon system more or less symmetrically. But here’s the problem: Newton’s equations also correctly predict the orbital altitude and velocity of objects orbiting the moon (such as the Apollo command module). The effect of the stars on a satellite orbiting the moon should be the same as it is on an object orbiting the earth. But objects orbiting the moon follow very different trajectories than they do when they orbit the earth. Their motion is related to the moon’s mass, just as Newton predicted.

Previous:

Of course. The only force acting on a satellite in orbit is the force of the earth’s gravity. It’s true that because earth’s mass isn’t uniformly distributed, there are minor fluctuations in the gravitational field, and this can cause minor variances in the satellite’s orbit. But that’s why satellites carry an onboard propulsion system with enough fuel to make minor adjustments to its orbit for many years.

You say, “Of course. The only force acting on a satellite in orbit is the force of the earth’s gravity,” but you don’t know that, you only assume it. Why can I say this? Two reasons: (1) You can’t explain what gravity is (all you have given is a mathematical formula of the results of some force that seems to attract objects), so how can you tell me Earth’s “gravity” is the only force acting on a satellite? (2) you have not provided anything to discount the forces of the stars as being a major factor in satellite operation. You’ve just assumed that all the forces are from the Earth, but you don’t know that.

I can easily prove that the stars can’t account for the motion of actual earth-orbiting satellites. You argue that the “forces of the stars” just happen to offset the force of earth’s gravity at 22,236 miles. If so, then objects below that point would be drawn toward the earth, objects above that point would be drawn away from the earth, and the geostationary satellites that are located precisely at that equilibrium point are suspended between the two forces. But this model is disproved by the orbit of the Chandra X-ray Observatory, shown below:

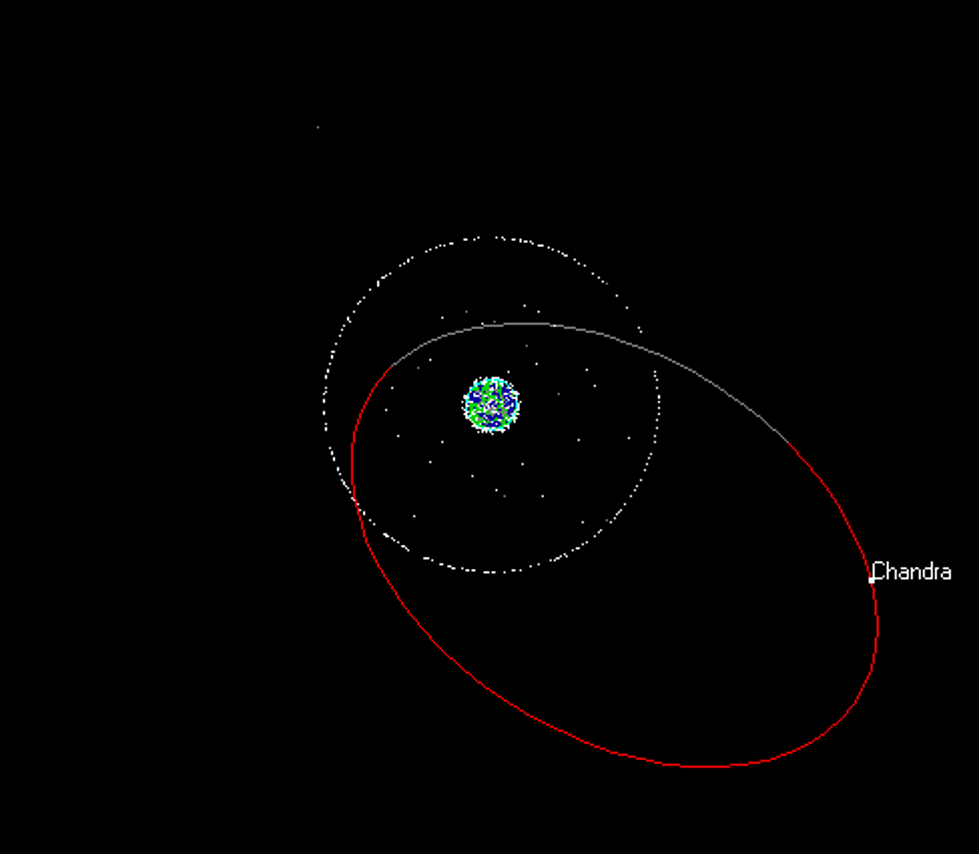
That satellite has a highly elliptical orbit whose perigee is at 86,487 miles – well beyond the alleged 22,236 mile equilibrium point. Now, if your theory were correct, when the Chandra satellite passes the point of equilibrium between the earth’s gravity and the inertial force from the stars (at 22,236 miles), it ought to keep right on going and never look back. But it doesn’t do that. At 86,487 miles, it turns around and heads back to earth. Therefore, even at that great distance, almost four times as far away from earth as the supposed equilibrium point between the earth’s gravity and the inertial force from the stars, the earth’s gravity is still strong enough to turn Chandra around and pull it back. But if the earth’s gravity is still strong enough at 86,487 miles to reverse the direction of a satellite that’s trying to run away, and pull it back to earth, it must also be true that at only 22,236 miles (four times closer to earth) the earth’s gravity would be easily strong enough to pull down the geostationary satellites, which aren’t speeding away from the earth, like Chandra, but are supposedly just sitting there.

It seems to me that the trajectory of the Chandra X-Ray Observatory offers a direct, empirical disproof of your theory. Clearly, there is no force at 22,236 miles sufficient to overpower the earth’s gravity and keep a satellite from being pulled down. If there were, it would also be sufficient to keep the earth’s gravity from turning Chandra around and pulling it down, especially since Chandra is four times farther away. Therefore, the fact that the geostationary satellites don’t fall proves that they are in orbit, as NASA has claimed all along, and the fact that they appear not to move relative to the surface of the earth proves that the earth is rotating.

Now let me take this opportunity to elaborate on the alternative to Newtonian mechanics - with a system that actually explains what Gravity is, rather than just put its results in mathematical formulas, as Newton did.

I’m all ears.

If the aether theory is correct, then Newton’s laws of gravitation need to be understood as the result of the effects of the aether. LaSage (1770) showed, mathematically and physically, that aether exerts a pressure on objects, e.g., pressure on spherical masses like the earth or the sun.

Question: If aether is an actual substance, like air, it will put a drag on spacecraft and planets flying through it, will it not?

On a single sphere the pressure is equal all around the sphere. But when two spherical objects come close to each other, one sphere will block some of the aether from colliding with the other, and vice-versa, which values are determined by their mass and shape.

Is this “aether” in motion? Where does it come from that two objects can “block” it from colliding with each other?

As I said earlier, the weight of an object on earth is determined by how many corpuscles of aether are hitting it from above as opposed to below.

If that is true, then shouldn’t I be able to increase my weight just by lying down, thus increasing the surface area of my body exposed to the aether? And shouldn’t I weigh the same on the moon as I do on the earth?

This also explains why atomic clocks in the upper atmosphere run 46,000 nanoseconds faster than at ground level. (Einstein attribute such anomalies to Relativity; non-Einsteinians attribute it to less dense aether). Because of its physical, not theoretical basis, the LaSage theory can account for the peculiar behavior of pendulums just before an eclipse or within deep mine shafts, and these movements were actually predicted by LaSage, whereas Newtonian and Einsteinian theories did not account for them. In fact, the ultrasensitive Cavendish torsion balance has detected discrepancies of up to .37% in the inverse square law proposed by Newton, yet accounted for by the LaSage model with no discrepancy. The Cavendish torsion balance has also calculated a variation in the speed of falling objects, opposite the Galileo “Pisa” experiment. Those objects that are elongated fall slower than those not elongated. The LaSage theory explains this, since the aether is hitting more surface area of the elongated object.

Again, if weight is determined by the surface area exposed to the aether, shouldn’t I be able to alter my weight just by altering my position? Is this why skydivers fall slower if they lie flat than if they dive straight down? Why doesn’t this work on a scale?

Previous:

Not really. Thrust is only required to maintain speed if there’s some force acting to retard that speed, which there isn’t in space. Once a satellite is accelerated to its proper orbital velocity by a booster rocket, its inertia will carry it around the earth for years. Haven’t you noticed that space stations like Mir and the International Space Station orbit the earth for decades even though they don’t have an engine?

Yes but they don’t maintain the same speed. The orbit decays bit by bit.

Yes, because of atmospheric drag on the vehicle.

The only reason Mir could stay up is that it kept lowering its orbit to compensate for the slowing of its speed. That would never work for a GSS that depends on keeping the same orbit so that it can transmit the same signals to Earth each second. For the GPS, I already quoted to you the statement from the Physics Today article which states that in order to keep a Keplerian orbit the GPS must speed up and slow down at regular intervals.

The GPS satellites are in much higher orbits than Mir. They won’t come down for a very long time.

Previous:

Well, that’s exactly what heliocentrism asserts. It asserts that the stars are an inertial frame of reference and that the earth moves and rotates within this frame. It is geocentrism that denies the stars form an inertial frame of reference. In geocentrism the earth itself is an inertial framework. Everything else is in non-inertial acceleration.

No, that’s not what I meant. I realize that heliocentrists refer to the “fixed stars,” but what I am saying is that they do not account for the forces of these cosmic masses on the principles of motion we see on earth.

Of course not. Remember that Newton’s law of gravitation tells us that the force of gravity is proportional to the product of the masses and inversely proportional to the square of the distance between them. It’s true that the stars are quite massive, but they’re so far away (except for the sun) that their effect is negligible.

Previous:

And I still say that unless you can prove the existence of a hypothetical gravitational force that just happens to precisely balance the earth’s gravity at an altitude of 22,240 miles, which by a remarkable coincidence is exactly the altitude at which a satellite would orbit the earth once a day, a stationary satellite over a stationary earth is an impossibility.

The Challenge was for you to prove your case.

I have done so. Your theory cannot account for the elliptical orbits of the geostationary satellites. Your only response has been a lot of hand-waving about magical forces that just happen to exist right where your theory has a gaping hole, and that just happen to be exactly as strong as you need them to be to close that hole. But even this lame attempt to prop up the geocentric theory is disproved by the Chandra X-ray Observatory, which orbits in a way that isn’t possible if you were right about the existence of a strong “gravitational and/or electromagnetic band” precisely 22,236 miles above the earth.

My contention is that no one can prove Heliocentrism, and therefore we are not obliged to interpret passages from the Bible concerning the sun’s movement as being metaphors; nor do we have to apologize for our Catholic Church when they officially rejected, by the mouths and signatures of two Popes, against Copernicanism; nor do we have to apologize for the Fathers of the Church as being nincompoops for believing that the sun went around the earth when they were going against the Greeks who espoused Heliocentrism.

Now I think we’re getting to the real issue. I strongly suspect that the real reason you think geocentrism is true has nothing to do with corpuscles of aether or Planck lengths, but it’s simply because you believe the Bible says the earth doesn’t move. Case closed. But I don’t agree. The Bible, like most literature, is full of phenomenological language. That is, it describes things according to their appearance. We do the same thing today when we speak of “sunrise” even though we don’t believe the sun actually rises. (Well, most of us don’t.) Likewise, the Bible says, for example, that the disciples had trouble staying awake because “their eyes were heavy” (Matt. 26:43). I don’t think this means their eyes literally weighed more than they weighed earlier in the day.

Regarding the opinions of those two popes, first I’d like to know which two popes you have in mind. And I would like for you to show me that they bound the Church to adhere to the geocentric system. Failing this, I’d simply say that getting elected Bishop of Rome doesn’t qualify one as an expert in cosmology. Our faith obliges us to assent to the teachings of the bishops in union with the pope when they speak definitively on matters of faith and morals, not math and science. However, if you think papal statements are determinative in this area, what do you make of Pope Urban VIII’s statement that the theory of the earth’s motion “had not been and could not be condemned as heretical” (See Encyclopedia Britannica, “Galileo”)? What do you make of the fact that Copernicus’ book was removed from the index of forbidden books in 1758?

As for the Fathers, I see no reason to view them as “nincompoops” because they believed in a geocentric universe (assuming they did). They probably believed lots of things that seem silly to us now. But so what? They were not scientists. They didn’t have geostationary satellites and Foucault pendulums. What they had was the deposit of the Christian faith, which was given to show us how to go to heaven, not how the heavens go (to paraphrase Cdl. Baronius). As St. Augustine put it, “One does not read in the Gospel that the Lord said: ’I will send you the Paraclete who will teach you about the course of the sun and moon.’ For he willed to make them Christians, not mathematicians.” I urge you to heed the warning of Pius XII in Divino Afflante Spiritu (1943) that the true sense of a biblical passage is not always obvious, as the sacred writers made full use of the idioms of their time and place.

Previous:

I don’t understand your use of terminology here. An “inertial framework” is simply a coordinate system that is not accelerating. Either it’s moving at a constant velocity, or it’s stationary. Therefore, I don’t understand what you mean when you say “the gravity of the stars . . . provide[s] the inertial framework for any moving object on or near the earth.” In a true inertial framework, all objects will obey the law of inertia and they won’t spontaneously change their velocity in response to apparent forces. Only real forces will alter their velocity. That’s yet another way we can demonstrate that the earth moves, by the way. The rotation of hurricanes, deflections in long-range projectile motion, etc., are caused by the “coriolis effect,” which is an inertial (i.e., apparent) force, the existence of which proves that the earth is not an inertial frame of reference but is in motion. If your theory were right, there would be no inertial forces on earth and it would be unnecessary to compensate for the earth’s rotation when targeting ICBMs, for example.

First, even if there was such a Coriolis effect, you have no way of proving whether it is attributable to the earth rotating or the stars rotating against a stationary earth. Second, the Coriolis force you are proposing has inherent contradictions. If you claim that projectiles must be adjusted due to the earth’s rotation, then this means that flying objects fly independently against the rotation of the earth.

On the contrary, the Coriolis effect requires that a projectile (or aircraft) moves with the earth’s rotation. As the projectile changes latitude, the velocity of the ground beneath it changes, leading to the so-called “Coriolis effect.”

If that is the case, then an airplane traveling from NY to LA, against the rotation of the earth, should arrive many hours before a plane traveling from LA to NY, but that is not the case.

Of course not.

All other things being equal, both planes take the same amount of time to arrive at their destination. Now some scientists try to explain this by claiming that the planes are within the “envelope” of the earth’s gravity, but then they have no explanation why ICBM’s, which are also in the “envelope,” must compensate for the earth’s rotation. (Yet I would submit that the textbooks which claim they are compensating for the Coriolis effect do so in the context of two moving objects, not against the Earth).

First of all, aircraft sitting on the ground rotate along with the earth. The atmosphere also rotates along with the earth. When an aircraft takes off it doesn’t suddenly stop relative to space while the earth rushes by at 1,000 mph. (Trust me on this, I have a pilot’s license). Further, according to The University of Brunswick Geodesy Group’s “Online Tutorial in Precision Navigation,” modern aircraft Integrated Navigation Systems do take into account the coriolis effect.

Here’s another variation of the same problem. If the Coriolis applies to the rotation of the earth, then why doesn’t the atmosphere (the clouds, especially) react in a Coriolis fashion relative to the Earth?

It does. It’s the rotation of the earth (and the Coriolis effect) that accounts for the large-scale circulation patterns in the atmosphere. For a detailed discussion of this see: http://wings.avkids.com/Book/Atmosphere/instructor/wind-01.html.

For example, if the earth is rotating at 1000 mph, should there not be a constant east-to-west drag on the atmosphere so that clouds are always moving at rapid speed from east to northwest, west, or southwest, but never from west to northeast, east, or southeast? Due to the your Coriolis effect, the clouds should always be moving away from us, and with motions at variance with the Earth. But that is not what we see. We often see clouds motionless in the sky for hours. How does modern physics explain this?

Simple. The atmosphere rotates along with the earth. Unequal heating of the atmosphere between the equator and the poles causes north-south circulation, and the rotation of the earth causes hemispherically-dependent rotational circulation.

They do so by claiming that the atmosphere is in an “inertial envelope” within the earth’s gravity. They are forced to this conclusion, for to postulate otherwise would leave them without an explanation for the movement of clouds. But if the atmosphere is in an “inertial envelope” with the earth, then how is that possible if projectiles shot from a stationary cannon must supposedly compensate for the Coriolis effect in order to hit their target? You can’t have it both ways, Gary. If the Coriolis effect is true for your concept of the cannon projectile, it must be true for the clouds, since both are within the earth’s gravitational envelope.

It is true for the clouds. It’s what causes hurricanes to rotate, and it’s what causes the general rotational circulation patterns in the atmosphere, as explained at the web page to which I referred above.

Previous:

At any rate, your claim that the gravity of the stars acts on “any moving object on or near the earth” is a disproof of your own theory. The stars move from east to west in both hemispheres, and therefore their gravity cannot account for the fact that the Coriolis effect works in the opposite direction in the southern hemisphere than it does in the northern hemisphere.

No one has ever proven that circular currents always go in opposite directions in the respective hemispheres, nor has anyone proven that the Coriolis causes said directions. That is a myth pure and simple.

Then it should be very easy for you to disprove. All you have to do is show me one hurricane that ever rotated clockwise in the Northern hemisphere, or counter-clockwise in the Southern hemisphere.

I have reams of documentation on that. It’s the same myth regarding water going down a drain counterclockwise in the northern hemisphere and clockwise in the southern hemisphere. It is a proven fact that water does not always go counterclockwise in the northern hemisphere and clockwise in the southern. The direction of spin has only to do with the shape of the container, the original direction of water, the tilt of the container, and other such ambient issues.

I know that. That’s why I mentioned hurricanes, not toilets. I’m well aware that Coriolis acceleration is much too subtle to have any impact on the flow of water in a sink. But it does affect large-scale events like hurricanes. As I said, if you can show me just one hurricane that rotated clockwise in the Northern hemisphere, or counter-clockwise in the Southern hemisphere, you will have proved your point.

Most honest scientists who know anything about Coriolis will tell you that the forces of Coriolis caused by a rotating earth would be much too small to effect the way water goes down a drain or how hurricanes form their direction.

It’s too small to effect water in a drain, but it does affect the rotation of hurricanes.

In fact, I just recently had a friend of mine in Australia do an experiment with his drain. He wrote back and told me that each time the water went down, in an undisturbed and level tank, it went counterclockwise the very direction you claim that is supposed to happen in the northern hemisphere only.

I make no such claim. I’m well aware that Coriolis acceleration is too subtle to effect the flow of water in a sink. But it certainly does affect intercontinental missiles and hurricanes.

There are tons of articles on this issue. Most scientists say it has nothing to do with Coriolis or a rotating earth.

If you’re talking about water in a sink, I agree. If you’re talking about the rotation of hurricanes, I say name some meteorologists who claim this has nothing to do with the rotation of the earth.

Previous:

Further, when the Apollo spacecraft went from the earth to the moon, its velocity was completely accounted for by the gravitational attraction of the earth and the moon. (The spacecraft was continuously decelerating as it moved away from the earth until it reached a point where the lunar gravity was stronger than the terrestrial gravity, at which point the spacecraft started to accelerate toward the moon). If the stars were exerting the same force on the Apollo spacecraft that they allegedly exert on a geosynchronous satellite, the Apollo spacecraft would have been going significantly faster than expected when it reached the moon.

Glad you brought this up, because using your own logic, the moon causes more problems for you than you think it does for me. There is a neutral gravity zone between the Earth and the Moon. NASA writes: “On a direct line from the Earth to the moon, equal gravitational effects would be found at approximately 216,000 miles, given a mean distance of 240,000 miles between the two bodies” (Wash, DC, 4-5-1990). Despite this, most scientists, in order to explain the tides, believe that the gravity of the moon somehow bursts through the neutral gravity zone (24,000 miles from the moon), and reaches all the way through the next 216,000 miles of earth’s gravity to grab hold of the earth’s water and pull it up each day!

The “neutral gravity zone” between the earth and the moon doesn’t mark the point where the moon’s gravity ceases to exist, it marks the point where the earth’s gravity becomes stronger. On the surface of the earth, the moon still exerts an influence, but it’s small compared to the influence of the earth’s gravity. That’s why the oceans just bulge a little; they don’t go flying off into space. For more on this, see: http://www.enchantedlearning.com/subjects/astronomy/moon/Tides.shtml.

Yet Franklyn Branley in The Moon: Earth’s Natural Satellite says: “The tide-raising force of the moon is very small indeed, compared to the force of gravity. The tide-raising force of the moon is about 1/9,000,000 that of the earth’s gravity” (p. 85). Gee! 9 million to one. Some force! That couldn’t even pick up a feather on the earth, let alone oceans of water. Obviously, gravity doesn’t explain the tides.

You fail to understand that the force of gravity is proportional to the product of the masses. Both the moon and the oceans are massive, therefore there’s significant gravitational attraction. A feather has almost no mass, and therefore the moon exerts almost no gravitational attraction on it.

Here’s another anomaly for you. The fact that the earth supposedly rotates at 1000 mph at its equator exerts a force on objects to fly off the earth.

That’s right, and that’s why the earth’s gravity is measurably lighter at the equator than it is at the poles. The acceleration of gravity at the poles is 9.83200 m/s2, but at the equator it’s 9.78100 m/s2. How does your system explain that?

Science claims that gravity holds the objects on the earth so they don’t fly off. But compare this. On the moon, the gravity is one sixth of the earth’s. Apparently, the men who walk on the moon need only a proportional amount of weight in their suits to simulate earth’s gravity. But the moon does not rotate and therefore there is no centrifugal force to throw them off, and therefore they would not need to have additional weight in their suits to reach a simulated earth gravity, since the centrifugal force created by going around at 1000 mph is far greater than one sixth the earth’s gravity. Gravity, without a compensating centrifugal force on the non-rotating moon, would flatten them like a pancake.

Wow, I’m impressed that you were able to cram so many errors into such a short paragraph. :-) Let’s take them in order. First of all, the Apollo spacesuits were not weighted to simulate earth gravity. Why would NASA want to make it more difficult for the astronauts to move around? And why would they want to lug all that useless weight to the moon? The Apollo spacesuits, complete with life-support system, weighed 180 lbs. on earth, which means they weighed only about 30 lbs. on the moon. According to Apollo 11 astronaut Buzz Aldrin, he and his spacesuit weighed 360 lbs. on earth, but only 60 lbs. on the moon. That’s why the astronauts were able to bounce around so effortlessly. Second, the moon does rotate – once a day in your system; once a month in mine. Third, the centrifugal force at the equator is only 3.38 cm/sec2, which is about three-tenths of one percent of the earth’s gravity. That’s not “far greater than one sixth of the earth’s gravity,” as you claimed; it’s far less than one sixth. Fourth, if a “compensating centrifugal force” were necessary to keep people from being squished by gravity, then the scientists who are at the south pole right now would be squished, because there’s no rotation, and thus no centrifugal force, at the poles. Things do weigh more at the poles, which is yet further proof that the earth rotates, but the effect isn’t all that dramatic.

What this means, Gary, is that in comparison with the non-rotating moon’s gravity, the earth cannot be rotating.

Nope, what it means is that the effect of the earth’s rotation is negligible compared with the pull of its gravity. The effect is measurable, which proves my case, but it’s still negligible.

Previous:

As I’ve already said, a satellite in orbit encounters almost no resistance to its motion, not from “centrifugal effects,” not from “coriolis effects,” and certainly not from “tidal forces of the stars,” which would be quite negligible given their distance. That’s why a space station like Russia’s Mir was able to stay in orbit for decades without an engine. There was almost no force acting against it to retard its motion. (Because of its relatively low altitude, there was some minuscule atmospheric drag on the station, which eventually brought it down, but if it had been orbiting at a geosynchronous altitude, it would have orbited probably forever.)

You have no way of proving what kept it up there. Your answer is inertia, but that is also a fictitious force.

Inertia is not a force. Inertia just means that a body in motion will tend to keep moving unless something acts to slow it down, speed it up, or change its path.

Newton never explained why a body had inertia or momentum.

He probably never explained why it has mass or dimension either. But did he need to? You prove the existence of inertia every time you step on the brakes in your car. Don’t you feel your body pulling forward against the seatbelt? That’s inertia.

Previous:

I don’t get it. You complain (wrongly) that orbital motion is caused by “centrifugal force,” which is a fictitious force, but then you explain the motion (or lack of it) of a geosynchronous satellite by appealing to “inertial force from the stars”? Surely you know that the phrase “inertial force” means “fictitious force,” don’t you?

In your system it is fictitious because you believe only in relative motion. You have no absolute motion in your system. You can’t have a real centrifugal force if you believe all bodies are in relative motion, since the supposed centrifugal force can be exchanged from one body to another. That’s what Einstein’s relativity is all about. But in my system, the centrifugal force is real, because I have one point in the universe which is stationary, and that is the Earth. Everything else moves. Thus, when I say the stars have an inertial force, that is because the stars are measured against a stationary Earth.

In my system I can easily take the stars to be fixed because their motion is so slow it would take generations to even notice it.

Previous:

At any rate, don’t you think it’s a rather remarkable coincidence that the alleged “inertial force from the stars” just happens to precisely balance the gravity of the earth at exactly the same altitude at which a satellite would orbit the earth once a day if the earth rotated? Doesn’t that raise a red flag for you? It sure does for me. Sounds like wishful thinking.

No, red flag. Your math works, but so does my math.

Not without appealing to imaginary forces that just happen to be exactly where you need them to be and exactly as strong as you need them to be.

But whose math represents reality is another story altogether. If the GSS can be explained from the perspective of Planck-dimension aether in a rotating universe — an aether that was supported by some of the best minds in physics until Einstein decided arbitrarily to reject that the earth was standing still - then I have no red flags at all.

In that case I’m eager to see how you explain the fact that non-orbiting satellites nevertheless have an apogee and a perigee.

But I’ll tell you who should have red flags, however. You! Unless you can adequately explain the anomalies of the GSS that I posed to you in the beginning of this essay (anti-Keplerian motion; Earth-fixed calculations in repositioning; Earth’s rotational perturbations) then I think it is you who has the problem.

I’ve explained all of it and more. I’ve also shown that geostationary satellites are in elliptical orbits that vary from one satellite to another and that cause the satellites to move slightly relative to the surface of the earth in a daily rhythm. I don’t think you can account for this, but I suspect you’ll try. I’m guessing you’ll claim it’s caused by vibrations in the aether or something.

All your system really has is mathematical formulas, but your system doesn’t explain much of how things work. You should also see a red flag when you notice that all the Church Fathers were Geocentrists;

None of them believed in germs either, but I’m still going to take my antibiotics.

the Church officially condemned Copernicanism by two Popes in formal decrees;

Wrong. The Church has never condemned Copernicanism. (See the Catholic Encyclopedia article on Galileo.) This is why I and other Catholics feel the need to oppose you on this topic. You are misrepresenting our faith and making it a laughingstock besides.

the Bible says the earth stands still and the sun moves;

Which, when you get right down to it, is what I think is your real reason for advocating geocentrism. You’re stuck in a fundamentalist mindset that ignores the Church’s own teachings about how to interpret Scripture.

Previous:

The moon does pull on the satellite, but the effect is negligible. Recall that the gravitational attraction between two bodies is proportional to the product of their masses, and inversely proportional to the square of the distance between them. The earth and the moon are both quite massive, and so they exert significant gravitational forces on each other. But a satellite’s mass is negligible in comparison. Telstar 6, for example, weights just 3,700 kg. Assuming that this satellite is orbiting at a geosynchronous altitude of 35,870 km, it’s easy to calculate that at the point in its orbit where it’s closest to the moon the gravitational force exerted on the satellite by the moon would be a whopping 15 grams. That’s half an ounce. And that’s why you can neglect the gravitational attraction of the moon when you plot a satellite’s orbit.

Half an ounce! Congratulations! You just wiped out science’s only explanation for the tides, since obviously, a 15 gram force could never lift millions of tons of water to make the tides on earth. Your system is just filled with these kinds of contradictions.

I said before that gravitational attraction is proportional to the product of the masses of the two objects. The mass of a satellite is negligible compared to the moon, and that’s why the gravitational attraction between them is only 15 grams. But the earth’s oceans are quite massive. The gravitational attraction between the moon and millions of tons of water is going to be significantly greater than the attraction between the moon and a little satellite.

Part 1, Part 2, Part 3